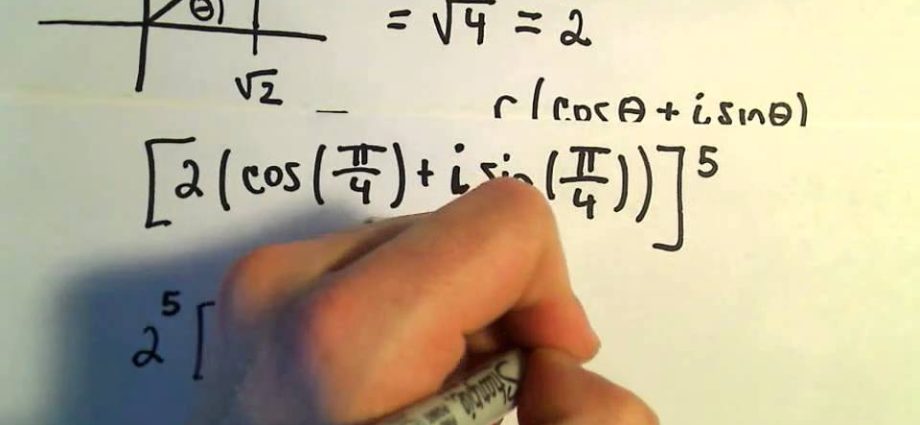複素数の自然べき乗

この出版物では、複素数を累乗する方法を検討します (De Moivre 公式の使用を含む)。 理論的な資料には、理解を深めるための例が添付されています。

複素数の累乗

まず、複素数には一般的な形式があることを思い出してください。 z = a + バイ (代数形式)。

これで、問題の解決に直接進むことができます。

平方数

次数を同じ因子の積として表して、それらの積を見つけることができます (そのことを思い出しながら)。 i² = -1).

z² = (a+bi)² = (ア + ビ)(ア + ビ)

例1：

z=3+5i

z² = (3+5i)² = (3 + 5i)(3 + 5i) = 9+15i+15i+25i² = -16 + 30i

また、合計の二乗を使用することもできます。

z² = (a+bi)² = a² + 2 ⋅ a ⋅ bi + (ビ)² = a² + 2abi – b²

注： 同様に、必要に応じて、差の XNUMX 乗、和/差の XNUMX 乗などの式を求めることができます。

N度

複素数を上げる z 現物 n 三角関数で表せば簡単です。

一般に、数値の表記は次のようになることを思い出してください。 z = |z| ⋅ (cos φ + i ⋅ sin φ).

累乗には、使用できます ド・モアブルの公式 (イギリスの数学者アブラハム・ド・モイヴルにちなんで名付けられました):

zⁿ = | z |ⁿ ⋅ (cos(nφ) + i ⋅ sin(nφ))

数式は、三角関数形式で記述することによって取得されます (モジュールが乗算され、引数が加算されます)。

例

複素数を上げる z = 2 ⋅ (cos 35° + i ⋅ sin 35°) XNUMX度まで。

ソリューション

z⁸ = 2⁸ ⋅ (cos(8 ⋅ 35°) + i ⋅ sin(8 ⋅ 35°)) = 256 ⋅ (cos 280° + i sin 280°).